힙 (heap)
- 완전 이진트리(complete binary tree)로서 다음 성질을 만족한다.
- 최소 힙(min heap): 각 노드의 값은 자식(child) 노드의 값보다 작거나 같다.
▷ 루트 노드가 최소값임
- 최대 힙(max heap): 각 노드의 값은 자식(child) 노드의 값보다 크거나 같다.
▷ 루트 노드가 최댓값임
힙 정렬
- 주어진 배열을 힙으로 만든 다음, 차례로 하나씩 힙에서 제거함으로써 정렬한다.
힙을 배열로 표현하면 아래와 같다.
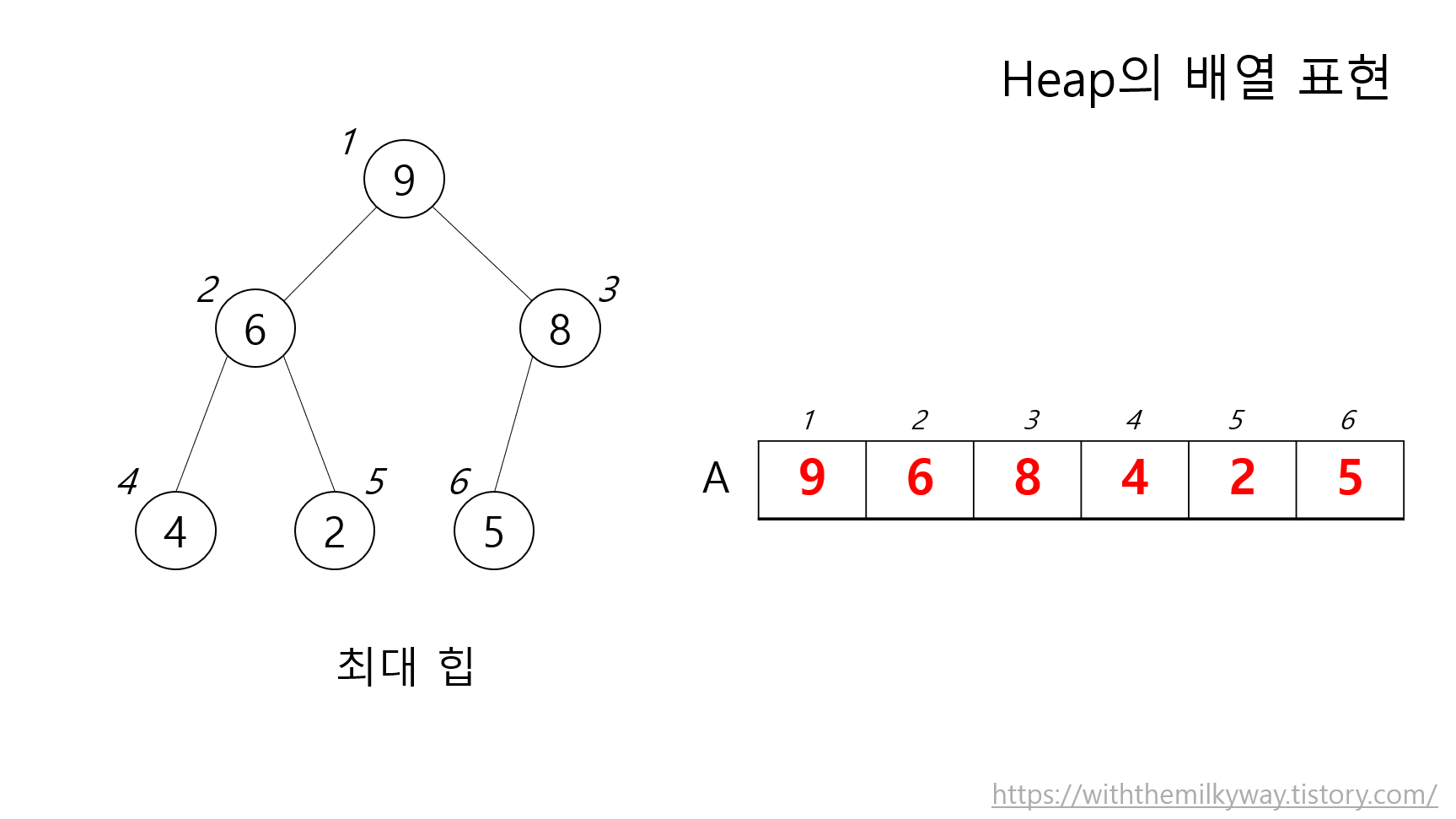
다음은 힙을 만드는 알고리즘이다.
buildHeap(A[], n) { // A[1...n]을 힙으로 만든다.
for i ← n/2 downto 1
heapify(A, i, n); // 힙 재구성
}
그리고 힙을 재구성하는 알고리즘이다.
heapify(A[], k, n) // n은 최대 인덱스
// A[k]의 두 자식을 루트로 하는 서브트리는 힙 성질을 이미 만족하고 있다.
// A[k]를 루트로 하는 트리를 힙 성질을 만족하도록 재구성한다.
{
// 큰 자식을 고른다.
left ← 2k; right ← 2k+1;
if(right <= n) then { // 자식이 둘인 경우
if(A[left] > A[right]) then bigger ← left; else bigger ← right;
}
else if(left <= n) then bigger ← left; // 왼쪽 자식만 있는 경우
else return; // 자식이 없는 경우 (종료)
// 큰 자식이 부모보다 크면 힙 성질 위반이므로 계속 재조정 작업
if(A[bigger] > A[k]) then {
A[k] ↔ A[bigger];
heapify(A, bigger, n);
}
}
힙 생성 후 오름차순으로 정렬한다.
heapSort(A[], n) { // A[1...n]을 힙 정렬 한다.
buildHeap(A, n); // 힙 만들기 : O(n log n)
for i ← n downto 2 { // : n-1 번 수행
A[1] ↔ A[i]; // 교환(A[1] 제거) : O(1)
heapify(A, 1, i-1); // 힙 재구성 : O(log n)
}
}
이와 같이 힙 정렬은 최악의 경우에도 O(n log n) 시간이 소요된다.
'Study > Algorithm' 카테고리의 다른 글
| [정렬] 계수 정렬(Counting Sort) (3) | 2020.04.16 |
|---|---|
| [정렬] 기수 정렬(Radix Sort) (5) | 2020.04.16 |
| [정렬] 퀵 정렬(Quick Sort) (3) | 2020.04.13 |
| [정렬] 병합 정렬(Merge Sort) (3) | 2020.04.13 |
| [정렬] 삽입 정렬(Insertion Sort) (6) | 2020.04.13 |
![[정렬] 힙 정렬(Heap Sort)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FvzoH6%2FbtqDmnFhhc4%2Fr9WIgvYJ0USjLfVsskqJO1%2Fimg.png)